Solving a cryptographic challenge in Rust

Howdy

Thought I’d kick things off by setting the tone for the rest of this blog. The front page description won’t do it justice as time passes and this nerdy diary of artless prose fills to the brim.

Getting closer to the point

This isn’t to say that the blog is purely tech-based or security-related. Indeed it will be a recurring theme, largely due to how much less effort it takes to type stuff (code) and then type some more (this blog) to discuss said stuff. But my other hobbies do plan on making an arrival here sooner rather than later. Patience, my fellow reader.

With that said, like comment subscribe hit the notification bell blah blah let’s get this show on the road!

The point

A long nine-month while back, during a CTF event in Dublin City run by Zero Days Security, I was stumped by one of the questions. The challenge Fast and Efficient came with a flag.enc file and a diagram illustrating how everything was set up.

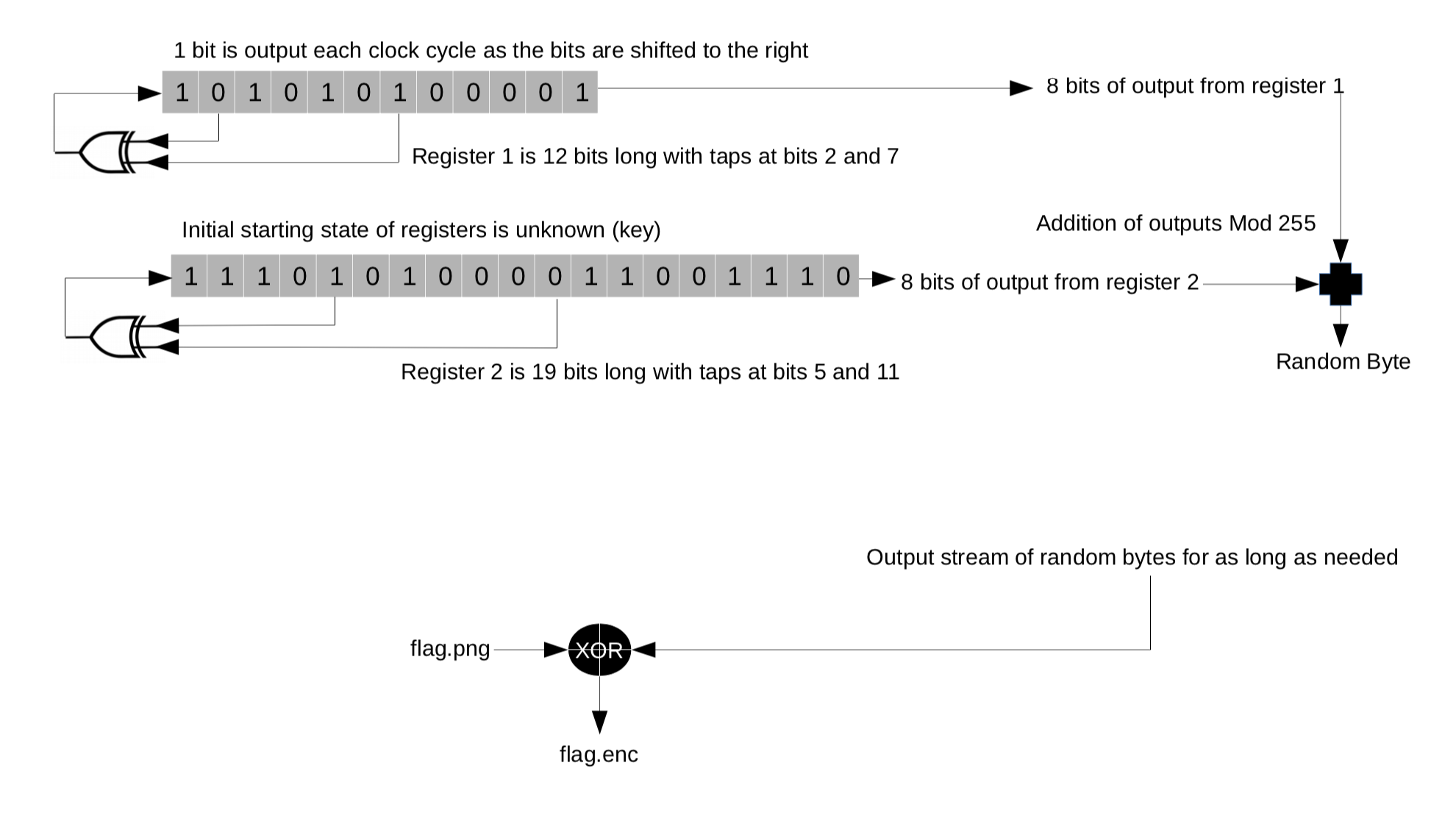
It shows two LFSRs (linear feedback shift registers) of different sizes being used as a keystream for encrypting a PNG file containing the flag. But I didn’t know how an LFSR worked and the internet wasn’t lending me a hand. So, what now? Good question!

Being the dumb-dumb that I was at the time, I tried looking around on GitHub to see what others have come up with to solve similar challenges, rather than actually trying to figure out what LFSRs are. To no avail. Luckily though, this problem remained unsolved for the entire duration of the competition, so my team managed to maintain our 2nd place position on the leaderboard.

Fast forward six months to October of 2019 when I revisited this question. I had spent a good portion of my summer break knee-deep in programming puzzles on Codewars and learning Rust as some sort of pursuit for knowledge and presumably eventual success, so you could say I was fresh out the oven to boldly take on a previously unsolved challenge like this one.

Understanding the problem

We have ourselves two registers, 12 and 19 bits long. What’s interesting is that we don’t know their starting state, and this unknown combination of ones and zeros is what makes the algorithm (supposedly) secure. Each register has two taps assigned. A tap is a bit that affects the next state of the register. For instance in this case the smaller register’s 2nd and 7th bits and the larger one’s 5th and 11th bits are taps.

Every round the register moves all of its bits to the right, the rightmost of which is not discarded, but rather appended to the output stream. Now the empty space on the left needs to be filled. That’s where the taps come in - they’re put through a linear function each round, storing the output bit in the leftmost empty space of the register. The function is usually a bitwise Exclusive OR (XOR) operation, as is in this scenario.

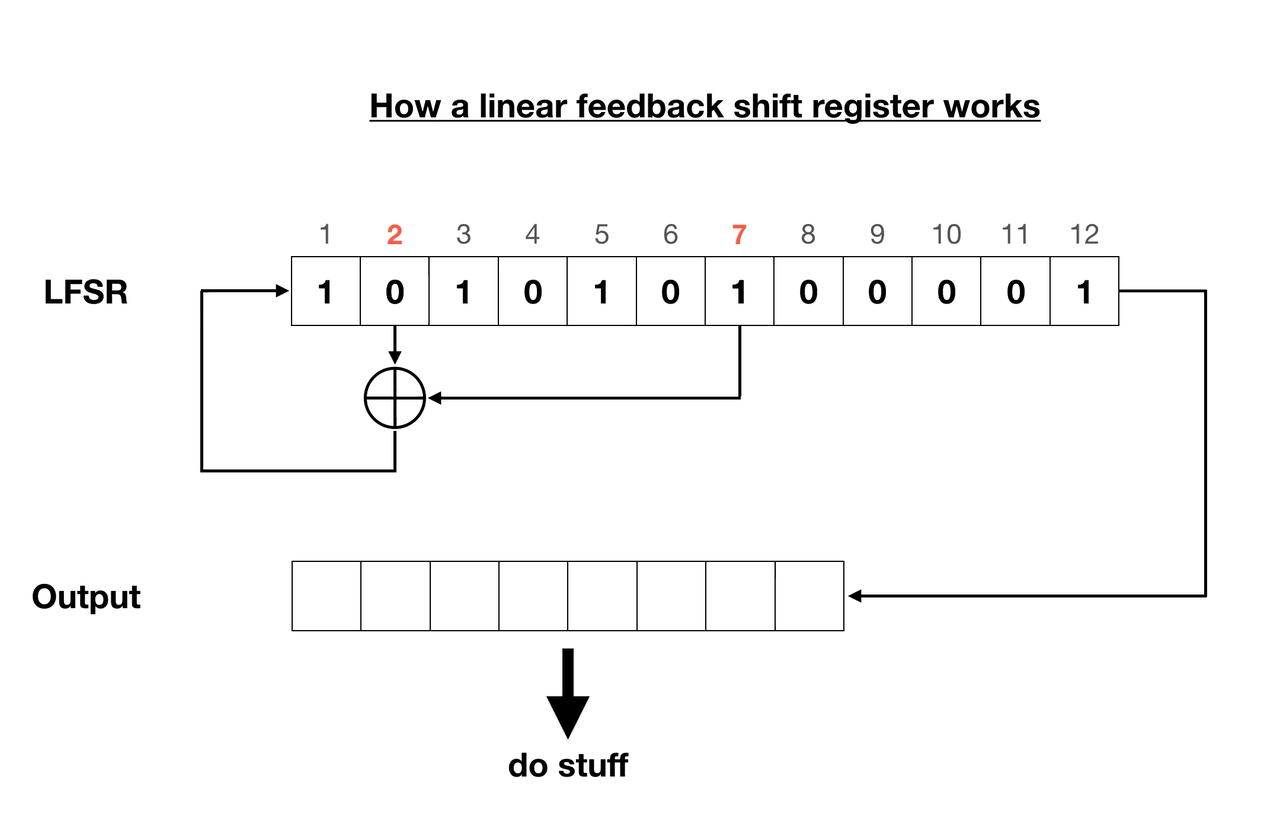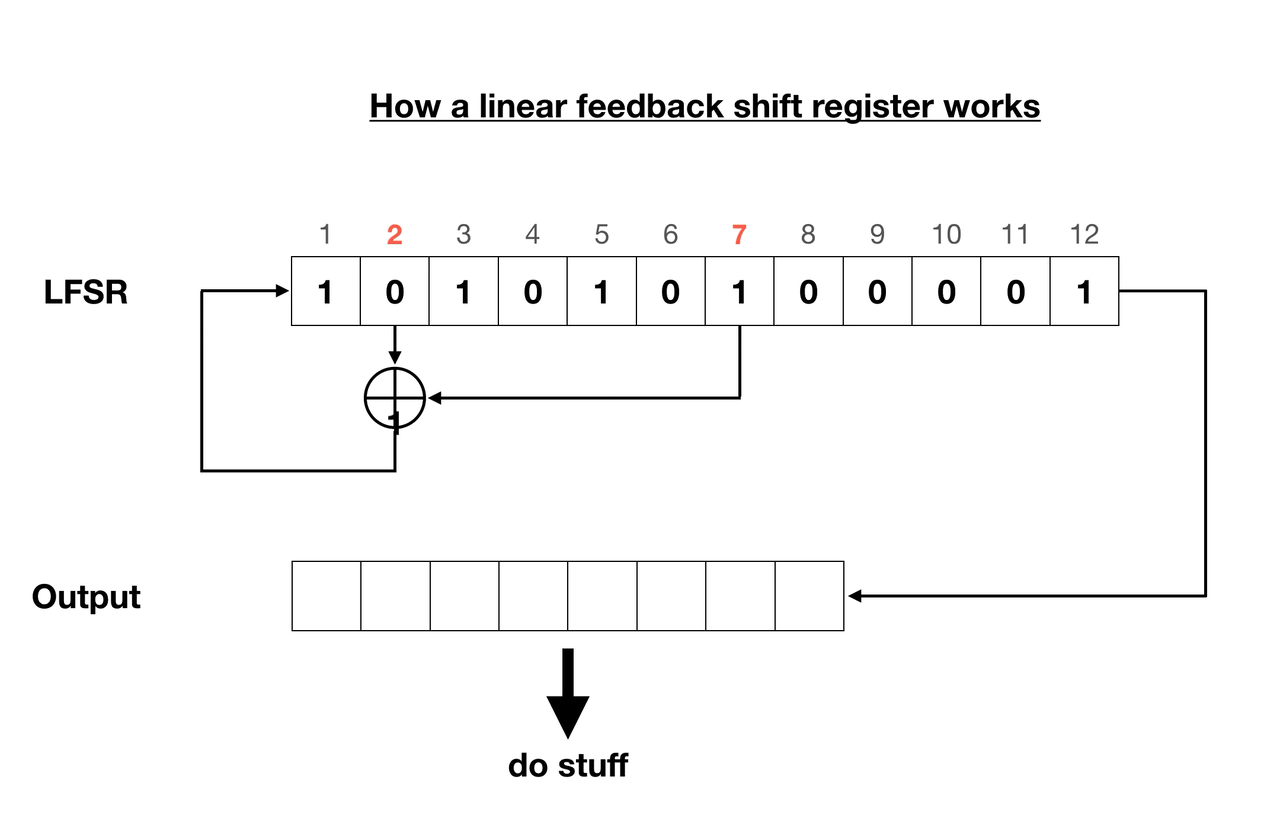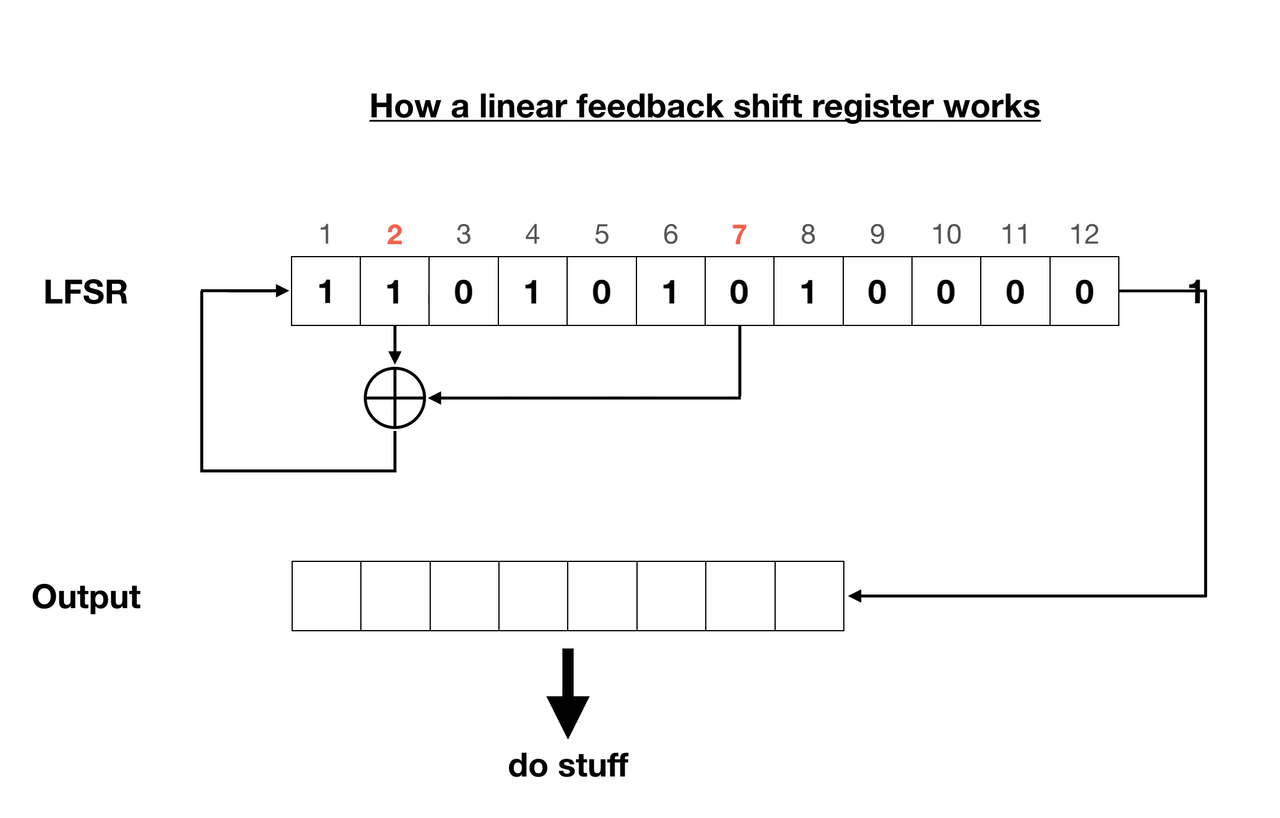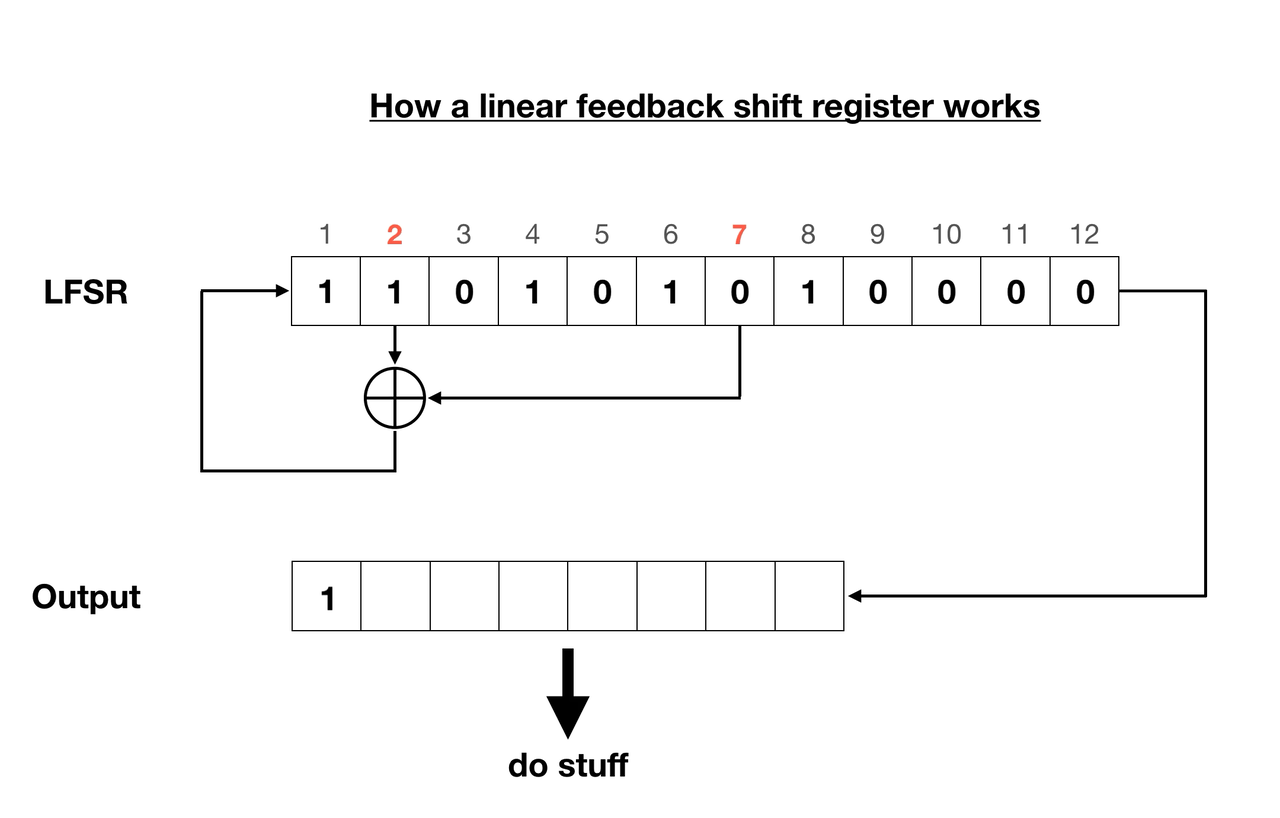
Each register cycles through eight rounds to output eight bits, also known as a byte. The two resulting bytes are added modulo 255. That’s right, not 256 oddly enough. This creates one final output byte, which is said to be part of a pseudo-random keystream. When XORed with the original flag.png file, the encrypted flag.enc is formed.

Our goal is to find out the seed value (starting position) of both registers, thus revealing the keystream and enabling the decryption of the flag file.

The “mod 255” part initially threw me off; it led me down a path of sleepless nights and fruitless attempts at correcting the challenge author’s “mistake” that was later revealed as an anti-plaigiarism technique. Worked wonders, didn’t it?

Finding the right approach

So anyway, before this turns into a tirade, I haphazardly put together a Python script to try and solve this dilemma, not realising how incredibly long it would take to loop over multiple highly abstracted operations for… hold on lemme do the maf 2^(12+19) = 2^31 = 2,147,483,648 …over 2 billion times! Sweet mother of… Python is certainly not the name of the game for this kinda job.

To the rescue comes my new friend Rust. I was ecstatic to finally put it to use, justifying all the procrastination and self-idulgence that I’d sacrificed to learn it over the summer. This was the moment to shine. Time to plot.

Plan of action

1. Set up 2 registers that match the criteria in the challenge diagram.
2. Loop over every possible seed value (starting point) of both registers.
3. Let N1,N2,N3,N4 be the first 4 bytes of the encrypted flag file.
4. Let K = (8 bits from register 1) + (8 bits from register 2) modulo 255.
   • Test if K ^ N1 is equal to the 1st byte of a PNG header, which is 0x89.
     • Do 8 further rounds to get a new K, and test if K ^ N2 equals 0x50.
       • Repeat for N3, testing for 0x4E.
         • Repeat for N4, testing for 0x47.
   • If any step fails, go back and try another seed value.
5. If four bytes are successfully decrypted, try the whole flag.enc file.

Execution time baby!

Time flies when you’re programming, and in my case most of it was compilation time as I sipped on my coffee and tweaked tad bits of code while the infamously sluggish compiler was running, in an attempt to up the efficiency factor by a couple notches. What a mouthful!

Long story short, I’ve just about had it with these unannounced peculiarities. It turns out that the specific implementation for LFSRs employed by this challenge discarded the first output bit. Thinking back to the competition, how was anyone expected to figure out this random quirk within 7 hours? Never mind the craze-filled vibe that filled the already cramped space as people ran about looking to get a decent LTE signal, or queueing for their 2 free team pizzas, all while another 50+ challenges also needed attention. Fun times :P

Eventually it came down to guessing and trying out of the ordinary things. Sometimes you just gotta have time, patience and a decent CPU, along with a hearty meal and a YouTube playlist to distract you from the dreadful compiler errors. Rustc knows that I’m kidding of course!

After grieving over all the time I lost, and over the time I spent grieving, and then some… I eventually came to a solución muy eficiente and compiled it with Rust’s superb optimisations. This resulted in code that brute forced over 2.1 billion combinations of bits in less than 30 seconds on my machine. Consistently.

Pretty neat, huh? Here’s the outcome:

“Whaa whaa just give me the code already”

Alright ya godforsaken beggars, the solution in its full glory, also found on my GitHub page with the rest of the files:

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110

use std::io;
use std::fs;
use std::io::prelude::*;
use std::convert::TryFrom;

fn main() {
    let mut done = 0; // Set to 1 on successful decryption
    let png: [u8;4] = [0x89, 0x50, 0x4E, 0x47]; // PNG magic bytes
    let (mut res, mut value): (u32, u8) = (0, 0); // Temporary vars

    // Set up registers with bit-length and mask
    let (l1, m1, l2, m2) = (12, 0b10000100000, 19, 0b100000100000000);
    let mut r1: Reg = Reg::new(l1, m1);
    let mut r2: Reg = Reg::new(l2, m2);

    let mut bytes: Vec<u8> = Vec::new(); // Vector for decrypted data
    let enc = get_encrypted_png(); // Encrypted data as Vec<u8>
    let metadata = fs::metadata("lfsr.png.enc").unwrap(); // Total bytes to
    let len = usize::try_from(metadata.len()).unwrap();   // be decrypted

    for i in r1.tap[0]..1<<l1 {
        //print!("\r{}", i);
        //io::stdout().flush().expect("Could not flush stdout!");
        for j in r2.tap[0]..1<<l2 {
            r1.set(i);
            r2.set(j);
            for level in 0..len {
                res = 0;
                for k in 0..8 {
                    res += (1 << k) * (r1.next() + r2.next());
                }
                res %= 255;
                //println!("Expected {} got {}", png[level] ^ enc[level], res);
                value = u8::try_from(res).unwrap();
                if level < 4 && value ^ enc[level] != png[level] {
                    break;
                }
                if level == 3 {
                    for x in {0..4} {
                        bytes.push(png[x]);
                    }
                    done = 1;
                }
                if level > 3 {
                    bytes.push(value ^ enc[level]);
                }
            }
            if done == 1 {
                //println!("\rSeeds: i, j = {}, {}", i, j);
                // https://stackoverflow.com/a/30838655
                let s: &[u8] = unsafe {
                    std::slice::from_raw_parts(
                        bytes.as_ptr() as *const u8,
                        bytes.len() * std::mem::size_of::<u8>()
                    )
                };
                let mut file = fs::File::create("lfsr.png").unwrap();
                file.write_all(s).unwrap();
                break;
            }
        }
        if done == 1 {
            break;
        }
    }
}

// https://stackoverflow.com/a/37189758
fn get_encrypted_png() -> Vec<u8> {
    let file = fs::File::open("lfsr.png.enc").expect("Failed to open!");
    let mut f = io::BufReader::new(file);
    let mut buf = Vec::<u8>::new();
    while f.read_until(b'\n', &mut buf).expect("Failed to read!") != 0 {}
    buf
}

struct Reg {
    tap: [u32; 2],
    length: usize,
    value: u32,
}

impl Reg {
    fn new(length: usize, mask: u32) -> Reg {
        let mut tap: [u32; 2] = [0, 0];
        let mut i = 0;
        for x in 0..length {
            if (mask >> x & 1) == 1 {
                tap[i] = u32::try_from(x).unwrap();
                i += 1;
            }
        }
        Reg { tap, length, value: 0 }
    }
    fn view(&self) {
        for i in {0..self.length}.rev() {
            //print!("{}", self.value >> i & 1);
        }
        //println!();
    }
    fn next(&mut self) -> u32 {
        let xor: u32 = ((self.value >> self.tap[0]) ^ (self.value >> self.tap[1])) & 1;
        //let old: u32 = self.value & 1;
        self.value = (self.value >> 1) ^ (xor << (self.length - 1));
        self.value & 1 //old
    }
    fn set(&mut self, value: u32) {
        self.value = value;
    }
}

Conclusion

It werks. Donut touch it. Also a special thanks to stackoverflow and my insomnia.